PCA Example
As one example of the power of the ParaCore Architect™, consider its use in building our FFT IP Core. One design application for this core involved generating a 2k x 2k-point FFT with a processing capability of 120 frames-per-second.
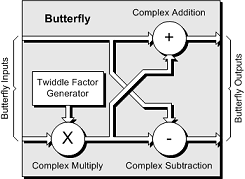
The smallest computational element used to generate an FFT is called a “butterfly”, which consists of a complex multiplication, a complex addition, and a complex subtraction generators.
The smallest computational element used to generate an FFT is called a “butterfly”, which consists of a complex multiplication, a complex addition, and a complex subtraction generators.
In turn, the complex multiplication requires four simple multiplications and two simple additions, while the complex addition and complex subtraction each require two simple additions. This means that each butterfly requires a total of four simple multiplications and six simple additions.
Processing a single 2,048 (2k) pixel row requires a total of 11,256 butterflies organized in eleven “ranks”, where the outputs from the butterflies forming the first rank are used to drive the butterflies forming the second rank, and so forth. Thus, processing a single row requires 45,025 simple multiplications and 67,536 simple additions. In order to generate the FFT for an entire 2k x 2k frame, this process has to be repeated for each of the 2,048 (2k) rows forming the frame. This means that in order to achieve a frame rate of 120 fps, the processing associated with each row must be completed within 4us. (This leads to a time budget of 90ps per simple multiplication and 60ps per simple addition.)
Let’s consider the 11,256 butterfly operations required to implement a 2k-point FFT. If execution time were not a major factor, it would only be necessary to use a Virtex-II XC2V40 device with its 4 x multiplier blocks, create a single butterfly structure (4 simple multipliers and 6 simple adders) and to cycle all of the butterfly operations through this butterfly function. The resulting structure would take 90us to generate each 2k-point FFT. However, although this is extremely respectable, it falls well short of the 4us time budget required by the image processing application discussed above.
The easiest way to increase the speed of this algorithm is to increase the number of butterfly structures instantiated in hardware and to perform more of the processing in parallel. In the case of XC2V6000 devices with 6 million system gates, 144 x 18-bit multipliers, and 144 x 18-kilobit RAM blocks, it’s possible to perform an entire 2k x 2k-point FFT fast enough to achieve a system that can process 120 frames-per-second. Furthermore, using XC2V10000 components allows the system to be scaled to achieve 240 frames-per-second.
The point is that targeting these different devices requires setting only a single ParaCore Architect parameter to specify the number of butterfly structures we require to be instantiated in hardware.
As another example, if we decide to change the length of the FFT from 2K to 1K points, setting a single parameter takes care of all of the details, including re-sizing the RAMS used to store any internal results. Similarly, another parameter can be used to select between fixed- and floating-point math formats (in the latter case, two further parameters are used to specify the size of the exponent and the mantissa).
Processing a single 2,048 (2k) pixel row requires a total of 11,256 butterflies organized in eleven “ranks”, where the outputs from the butterflies forming the first rank are used to drive the butterflies forming the second rank, and so forth. Thus, processing a single row requires 45,025 simple multiplications and 67,536 simple additions. In order to generate the FFT for an entire 2k x 2k frame, this process has to be repeated for each of the 2,048 (2k) rows forming the frame. This means that in order to achieve a frame rate of 120 fps, the processing associated with each row must be completed within 4us. (This leads to a time budget of 90ps per simple multiplication and 60ps per simple addition.)
Let’s consider the 11,256 butterfly operations required to implement a 2k-point FFT. If execution time were not a major factor, it would only be necessary to use a Virtex-II XC2V40 device with its 4 x multiplier blocks, create a single butterfly structure (4 simple multipliers and 6 simple adders) and to cycle all of the butterfly operations through this butterfly function. The resulting structure would take 90us to generate each 2k-point FFT. However, although this is extremely respectable, it falls well short of the 4us time budget required by the image processing application discussed above.
The easiest way to increase the speed of this algorithm is to increase the number of butterfly structures instantiated in hardware and to perform more of the processing in parallel. In the case of XC2V6000 devices with 6 million system gates, 144 x 18-bit multipliers, and 144 x 18-kilobit RAM blocks, it’s possible to perform an entire 2k x 2k-point FFT fast enough to achieve a system that can process 120 frames-per-second. Furthermore, using XC2V10000 components allows the system to be scaled to achieve 240 frames-per-second.
The point is that targeting these different devices requires setting only a single ParaCore Architect parameter to specify the number of butterfly structures we require to be instantiated in hardware.
As another example, if we decide to change the length of the FFT from 2K to 1K points, setting a single parameter takes care of all of the details, including re-sizing the RAMS used to store any internal results. Similarly, another parameter can be used to select between fixed- and floating-point math formats (in the latter case, two further parameters are used to specify the size of the exponent and the mantissa).